Lion Directional Planes Drawing Model
Introduction to Differential Equations
32 The Logistic Equation
Learning Objectives
- Draw the concept of ecology carrying capacity in the logistic model of population growth.
- Draw a direction field for a logistic equation and interpret the solution curves.
- Solve a logistic equation and interpret the results.
Differential equations can be used to represent the size of a population as it varies over fourth dimension. We saw this in an earlier chapter in the section on exponential growth and disuse, which is the simplest model. A more realistic model includes other factors that affect the growth of the population. In this department, we written report the logistic differential equation and see how information technology applies to the written report of population dynamics in the context of biology.
Population Growth and Carrying Capacity
To model population growth using a differential equation, we kickoff need to introduce some variables and relevant terms. The variable ![]() volition stand for fourth dimension. The units of time can be hours, days, weeks, months, or fifty-fifty years. Whatsoever given problem must specify the units used in that particular trouble. The variable
volition stand for fourth dimension. The units of time can be hours, days, weeks, months, or fifty-fifty years. Whatsoever given problem must specify the units used in that particular trouble. The variable ![]() will represent population. Since the population varies over time, it is understood to be a part of fourth dimension. Therefore nosotros utilize the notation
will represent population. Since the population varies over time, it is understood to be a part of fourth dimension. Therefore nosotros utilize the notation ![]() for the population every bit a function of time. If
for the population every bit a function of time. If ![]() is a differentiable function, then the commencement derivative
is a differentiable function, then the commencement derivative ![]() represents the instantaneous rate of change of the population as a function of fourth dimension.
represents the instantaneous rate of change of the population as a function of fourth dimension.
In Exponential Growth and Decay, we studied the exponential growth and decay of populations and radioactive substances. An case of an exponential growth part is ![]() In this function,
In this function, ![]() represents the population at time
represents the population at time ![]() represents the initial population (population at time
represents the initial population (population at time ![]() and the constant
and the constant ![]() is called the growth rate. (Effigy) shows a graph of
is called the growth rate. (Effigy) shows a graph of ![]() Here
Here ![]() and
and ![]()
An exponential growth model of population.
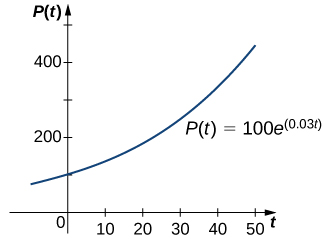
Nosotros can verify that the function ![]() satisfies the initial-value problem
satisfies the initial-value problem
![]()
This differential equation has an interesting estimation. The left-paw side represents the rate at which the population increases (or decreases). The right-hand side is equal to a positive constant multiplied by the current population. Therefore the differential equation states that the rate at which the population increases is proportional to the population at that point in fourth dimension. Furthermore, it states that the constant of proportionality never changes.
One trouble with this function is its prediction that as time goes on, the population grows without spring. This is unrealistic in a real-earth setting. Various factors limit the charge per unit of growth of a particular population, including birth rate, decease rate, nutrient supply, predators, and then on. The growth abiding ![]() normally takes into consideration the nativity and death rates but none of the other factors, and it tin can be interpreted as a net (nascence minus expiry) pct growth charge per unit per unit time. A natural question to ask is whether the population growth rate stays constant, or whether it changes over time. Biologists have found that in many biological systems, the population grows until a sure steady-land population is reached. This possibility is not taken into account with exponential growth. Still, the concept of carrying capacity allows for the possibility that in a given area, merely a certain number of a given organism or animal can thrive without running into resources issues.
normally takes into consideration the nativity and death rates but none of the other factors, and it tin can be interpreted as a net (nascence minus expiry) pct growth charge per unit per unit time. A natural question to ask is whether the population growth rate stays constant, or whether it changes over time. Biologists have found that in many biological systems, the population grows until a sure steady-land population is reached. This possibility is not taken into account with exponential growth. Still, the concept of carrying capacity allows for the possibility that in a given area, merely a certain number of a given organism or animal can thrive without running into resources issues.
Definition
The carrying capacity of an organism in a given surroundings is defined to be the maximum population of that organism that the surroundings can sustain indefinitely.
We use the variable ![]() to denote the carrying capacity. The growth rate is represented by the variable
to denote the carrying capacity. The growth rate is represented by the variable ![]() Using these variables, nosotros can define the logistic differential equation.
Using these variables, nosotros can define the logistic differential equation.
See this website for more than data on the logistic equation.
The logistic equation was first published by Pierre Verhulst in ![]() This differential equation can be coupled with the initial condition
This differential equation can be coupled with the initial condition ![]() to form an initial-value problem for
to form an initial-value problem for ![]()
Suppose that the initial population is pocket-sized relative to the conveying chapters. And then ![]() is minor, perhaps close to zero. Thus, the quantity in parentheses on the right-hand side of (Figure) is shut to
is minor, perhaps close to zero. Thus, the quantity in parentheses on the right-hand side of (Figure) is shut to ![]() and the right-manus side of this equation is shut to
and the right-manus side of this equation is shut to ![]() If
If ![]() so the population grows chop-chop, resembling exponential growth.
so the population grows chop-chop, resembling exponential growth.
However, equally the population grows, the ratio ![]() also grows, because
also grows, because ![]() is constant. If the population remains below the carrying capacity, then
is constant. If the population remains below the carrying capacity, then ![]() is less than
is less than ![]() so
so ![]() Therefore the right-manus side of (Figure) is withal positive, just the quantity in parentheses gets smaller, and the growth charge per unit decreases as a result. If
Therefore the right-manus side of (Figure) is withal positive, just the quantity in parentheses gets smaller, and the growth charge per unit decreases as a result. If ![]() then the right-paw side is equal to zero, and the population does not alter.
then the right-paw side is equal to zero, and the population does not alter.
At present suppose that the population starts at a value higher than the carrying capacity. Then ![]() and
and ![]() Then the right-hand side of (Figure) is negative, and the population decreases. As long as
Then the right-hand side of (Figure) is negative, and the population decreases. As long as ![]() the population decreases. It never actually reaches
the population decreases. It never actually reaches ![]() because
because ![]() volition go smaller and smaller, just the population approaches the carrying capacity as
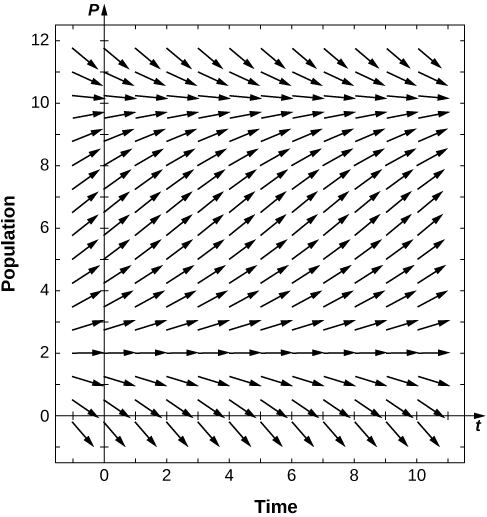
volition go smaller and smaller, just the population approaches the carrying capacity as ![]() approaches infinity. This assay can be represented visually past way of a phase line. A phase line describes the general behavior of a solution to an autonomous differential equation, depending on the initial status. For the example of a carrying capacity in the logistic equation, the phase line is as shown in (Figure).
approaches infinity. This assay can be represented visually past way of a phase line. A phase line describes the general behavior of a solution to an autonomous differential equation, depending on the initial status. For the example of a carrying capacity in the logistic equation, the phase line is as shown in (Figure).
A phase line for the differential equation ![]()

This phase line shows that when ![]() is less than nix or greater than
is less than nix or greater than ![]() the population decreases over time. When
the population decreases over time. When ![]() is between
is between ![]() and
and ![]() the population increases over time.
the population increases over time.
Chapter Opener: Examining the Carrying Capacity of a Deer Population
(credit: modification of work by Rachel Kramer, Flickr)

Permit's consider the population of white-tailed deer (Odocoileus virginianus) in the state of Kentucky. The Kentucky Department of Fish and Wild fauna Resources (KDFWR) sets guidelines for hunting and fishing in the state. Before the hunting flavor of ![]() it estimated a population of
it estimated a population of ![]() deer. Johnson notes: "A deer population that has plenty to swallow and is not hunted by humans or other predators will double every three years." (George Johnson, "The Problem of Exploding Deer Populations Has No Attractive Solutions," January
deer. Johnson notes: "A deer population that has plenty to swallow and is not hunted by humans or other predators will double every three years." (George Johnson, "The Problem of Exploding Deer Populations Has No Attractive Solutions," January ![]() accessed Apr nine, 2015, http://world wide web.txtwriter.com/onscience/Manufactures/deerpops.html.) This observation corresponds to a rate of increase
accessed Apr nine, 2015, http://world wide web.txtwriter.com/onscience/Manufactures/deerpops.html.) This observation corresponds to a rate of increase ![]() so the approximate growth rate is
so the approximate growth rate is
*** QuickLaTeX cannot compile formula: 23.11\text{%} *** Error message: File ended while scanning employ of \text@. Emergency cease. per year. (This assumes that the population grows exponentially, which is reasonable––at least in the curt term––with plentiful food supply and no predators.) The KDFWR also reports deer population densities for ![]() counties in Kentucky, the average of which is approximately
counties in Kentucky, the average of which is approximately ![]() deer per foursquare mile. Suppose this is the deer density for the whole state
deer per foursquare mile. Suppose this is the deer density for the whole state ![]() foursquare miles). The carrying chapters
foursquare miles). The carrying chapters ![]() is
is ![]() square miles times
square miles times ![]() deer per square mile, or
deer per square mile, or ![]() deer.
deer.
- For this awarding, we have
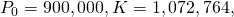 and
and 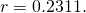 Substitute these values into (Effigy) and class the initial-value problem.
Substitute these values into (Effigy) and class the initial-value problem. - Solve the initial-value problem from part a.
- According to this model, what will be the population in
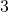 years? Recollect that the doubling time predicted by Johnson for the deer population was
years? Recollect that the doubling time predicted by Johnson for the deer population was 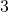 years. How do these values compare?
years. How do these values compare? - Suppose the population managed to attain
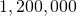 deer. What does the logistic equation predict will happen to the population in this scenario?
deer. What does the logistic equation predict will happen to the population in this scenario?
- The initial value problem is
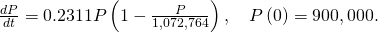
- The logistic equation is an democratic differential equation, and then we can utilize the method of separation of variables.
Step 1: Setting the right-mitt side equal to zero gives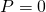 and
and 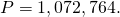 This means that if the population starts at zero information technology volition never change, and if information technology starts at the carrying capacity, it will never modify.
This means that if the population starts at zero information technology volition never change, and if information technology starts at the carrying capacity, it will never modify.
Step 2: Rewrite the differential equation and multiply both sides by:
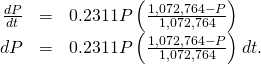
Divide both sides by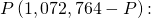
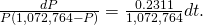
Step 3: Integrate both sides of the equation using fractional fraction decomposition:
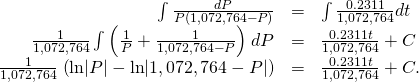
Pace 4: Multiply both sides by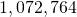 and utilise the quotient rule for logarithms:
and utilise the quotient rule for logarithms:
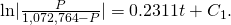
Here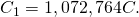 Adjacent exponentiate both sides and eliminate the absolute value:
Adjacent exponentiate both sides and eliminate the absolute value:
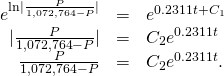
Hither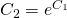 but after eliminating the absolute value, information technology can exist negative as well. At present solve for:
but after eliminating the absolute value, information technology can exist negative as well. At present solve for:

Step 5: To determine the value of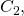 information technology is actually easier to get dorsum a couple of steps to where
information technology is actually easier to get dorsum a couple of steps to where 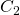 was divers. In particular, utilise the equation
was divers. In particular, utilise the equation
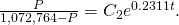
The initial status is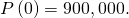 Replace
Replace 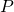 with
with 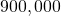 and
and 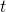 with zero:
with zero:
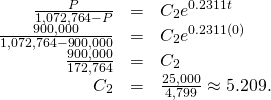
Therefore
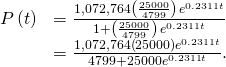
Dividing the numerator and denominator by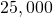 gives
gives
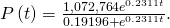
(Figure) is a graph of this equation.
Logistic bend for the deer population with an initial population of
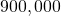 deer.
deer.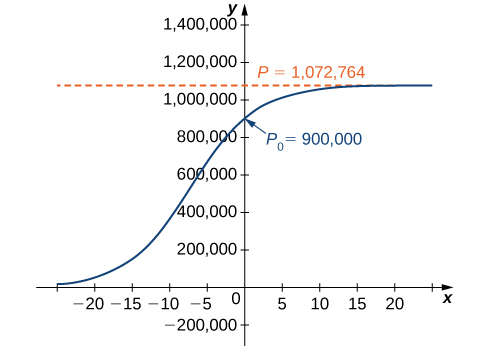
- Using this model nosotros can predict the population in
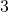 years.
years.
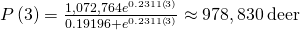
This is far short of twice the initial population of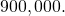 Remember that the doubling time is based on the assumption that the growth rate never changes, but the logistic model takes this possibility into account.
Remember that the doubling time is based on the assumption that the growth rate never changes, but the logistic model takes this possibility into account. - If the population reached
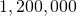 deer, then the new initial-value problem would be
deer, then the new initial-value problem would be
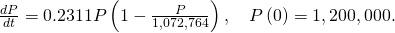
The general solution to the differential equation would remain the aforementioned.
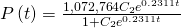
To determine the value of the constant, return to the equation
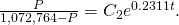
Substituting the values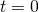 and
and 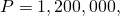 you get
you get
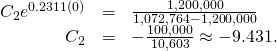
Therefore
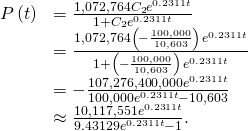
This equation is graphed in (Figure).
Logistic curve for the deer population with an initial population of
 deer.
deer.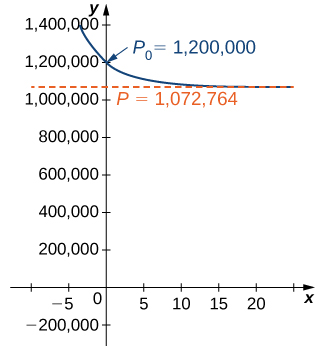
Solving the Logistic Differential Equation
The logistic differential equation is an democratic differential equation, so we tin use separation of variables to find the general solution, every bit nosotros just did in (Figure).
Footstep one: Setting the correct-mitt side equal to zero leads to ![]() and
and ![]() as constant solutions. The outset solution indicates that when in that location are no organisms present, the population will never grow. The second solution indicates that when the population starts at the carrying capacity, it will never modify.
as constant solutions. The outset solution indicates that when in that location are no organisms present, the population will never grow. The second solution indicates that when the population starts at the carrying capacity, it will never modify.
Footstep 2: Rewrite the differential equation in the grade
![]()
Then multiply both sides by ![]() and divide both sides by
and divide both sides by ![]() This leads to
This leads to
![]()
Multiply both sides of the equation by ![]() and integrate:
and integrate:
![]()
The left-hand side of this equation can be integrated using partial fraction decomposition. Nosotros exit information technology to you to verify that
![]()
Then the equation becomes
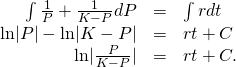
Now exponentiate both sides of the equation to eliminate the natural logarithm:
![]()
We define ![]() and so that the equation becomes
and so that the equation becomes
![]()
To solve this equation for ![]() first multiply both sides past
first multiply both sides past ![]() and collect the terms containing
and collect the terms containing ![]() on the left-mitt side of the equation:
on the left-mitt side of the equation:
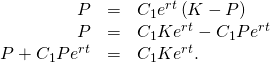
Next, factor ![]() from the left-hand side and split up both sides by the other gene:
from the left-hand side and split up both sides by the other gene:
![]()
The last step is to determine the value of ![]() The easiest way to do this is to substitute
The easiest way to do this is to substitute ![]() and
and ![]() in identify of
in identify of ![]() in (Figure) and solve for
in (Figure) and solve for ![]()
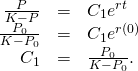
Finally, substitute the expression for ![]() into (Figure):
into (Figure):
![]()
Now multiply the numerator and denominator of the correct-hand side by ![]() and simplify:
and simplify:
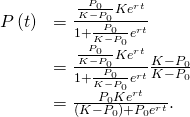
We state this event equally a theorem.
Solution of the Logistic Differential Equation
Consider the logistic differential equation subject to an initial population of ![]() with carrying capacity
with carrying capacity ![]() and growth rate
and growth rate ![]() The solution to the corresponding initial-value trouble is given past
The solution to the corresponding initial-value trouble is given past
![]()
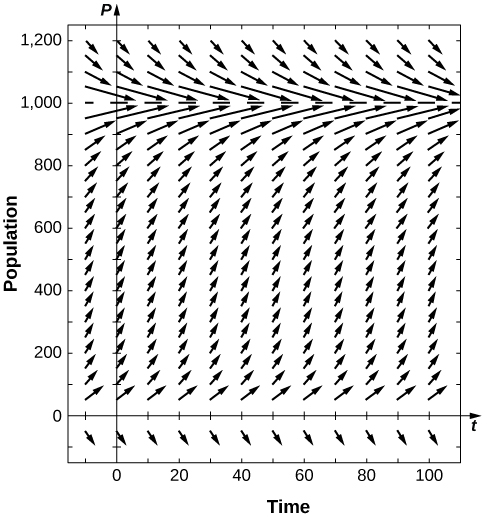
Now that nosotros have the solution to the initial-value problem, we can choose values for ![]() and
and ![]() and study the solution curve. For example, in (Effigy) we used the values
and study the solution curve. For example, in (Effigy) we used the values ![]() and an initial population of
and an initial population of ![]() deer. This leads to the solution
deer. This leads to the solution
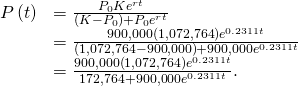
Dividing tiptop and bottom past ![]() gives
gives
![]()
This is the aforementioned every bit the original solution. The graph of this solution is shown once again in blue in (Figure), superimposed over the graph of the exponential growth model with initial population ![]() and growth rate
and growth rate ![]() (appearing in greenish). The ruddy dashed line represents the carrying chapters, and is a horizontal asymptote for the solution to the logistic equation.
(appearing in greenish). The ruddy dashed line represents the carrying chapters, and is a horizontal asymptote for the solution to the logistic equation.
A comparison of exponential versus logistic growth for the same initial population of ![]() organisms and growth charge per unit of
organisms and growth charge per unit of
*** QuickLaTeX cannot compile formula: 23.eleven\text{%}. *** Error message: File ended while scanning use of \text@. Emergency terminate. 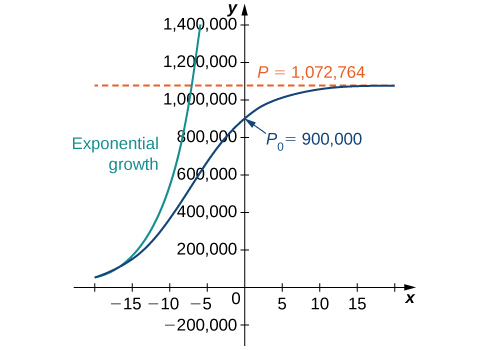
Working under the assumption that the population grows according to the logistic differential equation, this graph predicts that approximately ![]() years earlier
years earlier ![]() the growth of the population was very close to exponential. The net growth charge per unit at that time would accept been around
the growth of the population was very close to exponential. The net growth charge per unit at that time would accept been around
*** QuickLaTeX cannot compile formula: 23.1\text{%} *** Error bulletin: File ended while scanning utilize of \text@. Emergency stop. per year. Equally fourth dimension goes on, the two graphs separate. This happens because the population increases, and the logistic differential equation states that the growth rate decreases as the population increases. At the time the population was measured ![]() it was close to carrying chapters, and the population was starting to level off.
it was close to carrying chapters, and the population was starting to level off.
The solution to the logistic differential equation has a point of inflection. To find this betoken, ready the 2nd derivative equal to zero:
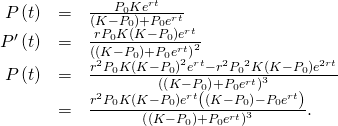
Setting the numerator equal to cipher,
![]()
As long as ![]() the unabridged quantity before and including
the unabridged quantity before and including ![]() is nonzero, so we tin can divide information technology out:
is nonzero, so we tin can divide information technology out:
![]()
Solving for ![]()
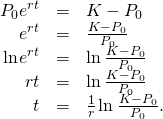
Observe that if ![]() then this quantity is undefined, and the graph does not have a point of inflection. In the logistic graph, the point of inflection can be seen every bit the betoken where the graph changes from concave up to concave down. This is where the "leveling off" starts to occur, because the net growth rate becomes slower as the population starts to approach the conveying capacity.
then this quantity is undefined, and the graph does not have a point of inflection. In the logistic graph, the point of inflection can be seen every bit the betoken where the graph changes from concave up to concave down. This is where the "leveling off" starts to occur, because the net growth rate becomes slower as the population starts to approach the conveying capacity.
-
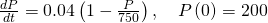
-
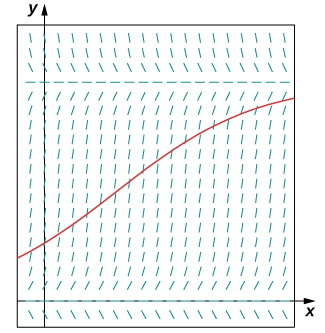
-
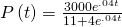
-
After
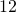 months, the population will exist
months, the population will exist 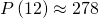 rabbits.
rabbits.
Hint
Beginning determine the values of ![]() and
and ![]() And then create the initial-value problem, draw the direction field, and solve the trouble.
And then create the initial-value problem, draw the direction field, and solve the trouble.
Pupil Project: Logistic Equation with a Threshold Population
An improvement to the logistic model includes a threshold population. The threshold population is defined to be the minimum population that is necessary for the species to survive. Nosotros use the variable ![]() to stand for the threshold population. A differential equation that incorporates both the threshold population
to stand for the threshold population. A differential equation that incorporates both the threshold population ![]() and carrying chapters
and carrying chapters ![]() is
is
![]()
where ![]() represents the growth rate, as earlier.
represents the growth rate, as earlier.
- The threshold population is useful to biologists and can be utilized to determine whether a given species should exist placed on the endangered list. A group of Australian researchers say they have adamant the threshold population for whatever species to survive:
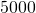 adults. (Catherine Clabby, "A Magic Number," American Scientist 98(1): 24, doi:10.1511/2010.82.24. accessed Apr nine, 2015, http://www.americanscientist.org/issues/pub/a-magic-number). Therefore we utilize
adults. (Catherine Clabby, "A Magic Number," American Scientist 98(1): 24, doi:10.1511/2010.82.24. accessed Apr nine, 2015, http://www.americanscientist.org/issues/pub/a-magic-number). Therefore we utilize 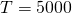 as the threshold population in this projection. Suppose that the environmental carrying capacity in Montana for elk is
as the threshold population in this projection. Suppose that the environmental carrying capacity in Montana for elk is 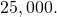 Set up (Effigy) using the carrying capacity of
Set up (Effigy) using the carrying capacity of 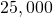 and threshold population of
and threshold population of 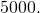 Assume an annual cyberspace growth rate of
Assume an annual cyberspace growth rate of *** QuickLaTeX cannot compile formula: 18\text{%}. *** Mistake message: File ended while scanning use of \text@. Emergency stop. - Draw the management field for the differential equation from step
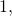 along with several solutions for unlike initial populations. What are the constant solutions of the differential equation? What do these solutions correspond to in the original population model (i.e., in a biological context)?
along with several solutions for unlike initial populations. What are the constant solutions of the differential equation? What do these solutions correspond to in the original population model (i.e., in a biological context)? - What is the limiting population for each initial population you chose in step
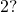 (Hint: use the slope field to encounter what happens for various initial populations, i.east., look for the horizontal asymptotes of your solutions.)
(Hint: use the slope field to encounter what happens for various initial populations, i.east., look for the horizontal asymptotes of your solutions.) - This equation can be solved using the method of separation of variables. Even so, it is very difficult to get the solution every bit an explicit function of
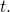 Using an initial population of
Using an initial population of 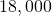 elk, solve the initial-value problem and express the solution as an implicit function of
elk, solve the initial-value problem and express the solution as an implicit function of 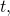 or solve the general initial-value problem, finding a solution in terms of
or solve the general initial-value problem, finding a solution in terms of 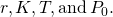
Key Concepts
- When studying population functions, different assumptions—such equally exponential growth, logistic growth, or threshold population—lead to different rates of growth.
- The logistic differential equation incorporates the concept of a carrying capacity. This value is a limiting value on the population for whatsoever given environment.
- The logistic differential equation can be solved for whatever positive growth charge per unit, initial population, and conveying capacity.
Central Equations
For the post-obit problems, consider the logistic equation in the form ![]() Depict the directional field and notice the stability of the equilibria.
Depict the directional field and notice the stability of the equilibria.
![]()
![]()
Solve the logistic equation for ![]() and an initial condition of
and an initial condition of ![]()
![]()
Solve the logistic equation for ![]() and an initial status of
and an initial status of ![]()
A population of deer within a park has a conveying chapters of ![]() and a growth rate of
and a growth rate of
*** QuickLaTeX cannot compile formula: 2\text{%}. *** Error bulletin: File ended while scanning use of \text@. Emergency stop. If the initial population is ![]() deer, what is the population of deer at any given fourth dimension?
deer, what is the population of deer at any given fourth dimension?
![]()
The following problems consider the logistic equation with an added term for depletion, either through death or emigration.
[T] The population of trout in a pond is given by ![]() where
where ![]() trout are caught per year. Use your computer or estimator software to draw a directional field and describe a few sample solutions. What practise you expect for the behavior?
trout are caught per year. Use your computer or estimator software to draw a directional field and describe a few sample solutions. What practise you expect for the behavior?
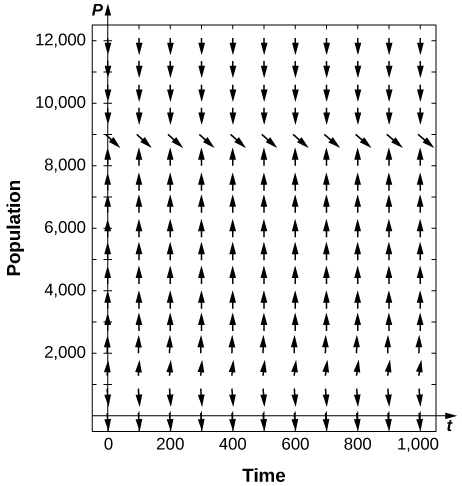
In the preceding problem, what are the stabilities of the equilibria ![]()
[T] For the preceding trouble, use software to generate a directional field for the value ![]() What are the stabilities of the equilibria?
What are the stabilities of the equilibria?
![]() semi-stable
semi-stable
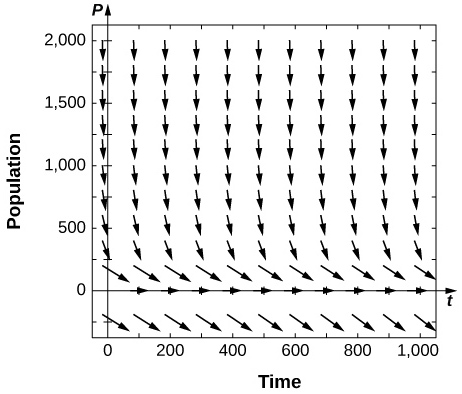
[T] For the preceding problems, use software to generate a directional field for the value ![]() What are the stabilities of the equilibria?
What are the stabilities of the equilibria?
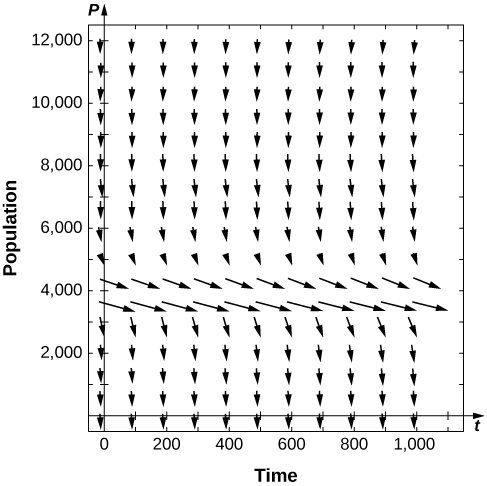
[T] For the preceding problems, consider the instance where a certain number of fish are added to the pond, or ![]() What are the nonnegative equilibria and their stabilities?
What are the nonnegative equilibria and their stabilities?
![]() stable
stable
It is more likely that the amount of fishing is governed by the electric current number of fish present, so instead of a constant number of fish being caught, the rate is proportional to the current number of fish present, with proportionality constant ![]() equally
equally
![]()
[T] For the previous angling problem, draw a directional field assuming ![]() Draw some solutions that exhibit this behavior. What are the equilibria and what are their stabilities?
Draw some solutions that exhibit this behavior. What are the equilibria and what are their stabilities?
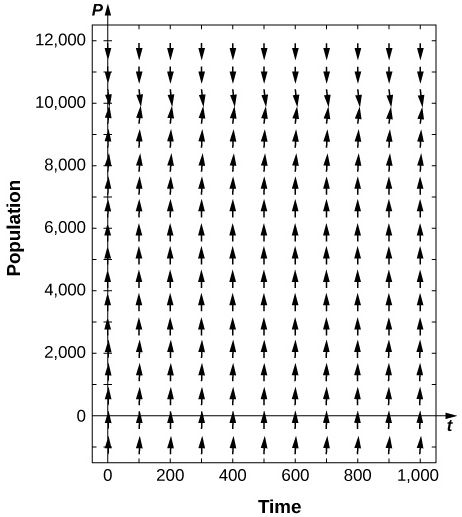
[T] Use software or a calculator to draw directional fields for ![]() What are the nonnegative equilibria and their stabilities?
What are the nonnegative equilibria and their stabilities?
![]() is semi-stable
is semi-stable
[T] Use software or a calculator to draw directional fields for ![]() What are the equilibria and their stabilities?
What are the equilibria and their stabilities?
Solve this equation, assuming a value of ![]() and an initial condition of
and an initial condition of ![]() fish.
fish.
![]()
Solve this equation, assuming a value of ![]() and an initial condition of
and an initial condition of ![]() fish.
fish.
The following problems add in a minimal threshold value for the species to survive, ![]() which changes the differential equation to
which changes the differential equation to ![]()
Draw the directional field of the threshold logistic equation, assuming ![]() When does the population survive? When does it go extinct?
When does the population survive? When does it go extinct?
For the preceding trouble, solve the logistic threshold equation, assuming the initial status ![]()
The following questions consider the Gompertz equation, a modification for logistic growth, which is oft used for modeling cancer growth, specifically the number of tumor cells.
The Gompertz equation is given past ![]() Describe the directional fields for this equation assuming all parameters are positive, and given that
Describe the directional fields for this equation assuming all parameters are positive, and given that ![]()
Assume that for a population, ![]() and
and ![]() Draw the directional field associated with this differential equation and draw a few solutions. What is the behavior of the population?
Draw the directional field associated with this differential equation and draw a few solutions. What is the behavior of the population?
Show that the population grows fastest when information technology reaches half the conveying capacity for the logistic equation ![]()
When does population increase the fastest in the threshold logistic equation ![]()
![]()
When does population increase the fastest for the Gompertz equation ![]()
Below is a table of the populations of whooping cranes in the wild from ![]() The population rebounded from near extinction afterwards conservation efforts began. The post-obit issues consider applying population models to fit the data. Assume a carrying capacity of
The population rebounded from near extinction afterwards conservation efforts began. The post-obit issues consider applying population models to fit the data. Assume a carrying capacity of ![]() cranes. Fit the data assuming years since
cranes. Fit the data assuming years since ![]() (so your initial population at fourth dimension
(so your initial population at fourth dimension ![]() would be
would be ![]() cranes).
cranes).
| Year (years since conservation began) | Whooping Crane Population |
|---|---|
| | |
| | |
| | |
| | |
| | |
| | |
| | |
Notice the equation and parameter ![]() that best fit the data for the logistic equation.
that best fit the data for the logistic equation.
![]()
Find the equation and parameters ![]() and
and ![]() that all-time fit the data for the threshold logistic equation.
that all-time fit the data for the threshold logistic equation.
Find the equation and parameter ![]() that all-time fit the information for the Gompertz equation.
that all-time fit the information for the Gompertz equation.
![]()
Graph all three solutions and the data on the same graph. Which model appears to be most accurate?
Source: https://opentextbc.ca/calculusv2openstax/chapter/the-logistic-equation/
0 Response to "Lion Directional Planes Drawing Model"
Publicar un comentario